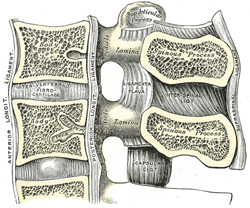Fig. 1: Sagittal section throught the human lumbar vertebral spine. Facet joints are shown right. The ligaments shown are intertransverse ligament (ITL), supraspinous ligament (SSL), interspinous ligament (ISL), ligamentum flavum (LF), anterior longitudinal ligament (ALL), posterior longitudinal ligament (PLL) and capsular ligament (CL).

The curvature of vertebral facet joints may play an important role in the study of load bearing characteristics and clinical interventions such as graded facetectomy. In previously published finite element simulations of this procedure, the curvature was either neglected or approximated with a varying degree of accuracy. Here we study the effect of the curvature in three different load situations by using a numerical model which is able to represent the actual curvature without any loss of accuracy. The results show that previously used approximations of the curvature lead to good results in the analysis of sagittal moment/rotation. However, for sagittal shear-force/displacement and for the contact stress distribution, previous results deviate significantly from our results. These findings are supported through related convergence studies. Hence we can conclude that in order to obtain reliable results for the analysis of sagittal shear-force/displacement and the contact stress distribution in the facet joint, the curvature must not be neglected. This is of particular importance for the numerical simulation of the spine, which may lead to improved diagnostics, effective surgical planning and intervention. The proposed method may represent a more reliable basis to optimize the biomedical engineering design for tissue engineering or, for example, for spinal implants.

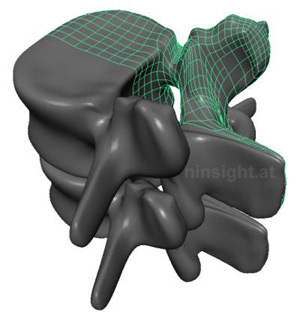Fig. 2: Contact interaction between lumbar vertebral bodies L4 and L5. Representation of both bodies by means of subdivision surfaces. The ligaments and the intervertebral disc are not show,

The geometry of the human vertebrae, and, in particular, the curvature of the facet joints, is highly complex. For our study we have not achieved the desired accuracy with CT-image-based analyses. Hence, we used slices from the Visible-Human-Data project [1]. The slices were available in distances of 1 mm. The accurate consideration of the facet geometry in the finite element simulation requires a special technique for mesh generation and surface description. Therefore, the geometry of L2 to L5 was traced with so called subdivision surfaces [2]. They help to model smooth biological surfaces up to any level of accuracy, similarly to NURBS, Bézier or Hermite splines. However, their advantage is that they can deal with arbitrary mesh topologies, i.e. more or less than four quadrilaterals can meet in one node. Such a geometrical situation is encountered quite frequently, and can not be treated easily with NURBS, Bézier or Hermite splines.
In contrast, previous studies represented the facet joints as planar surfaces, which are described by their angular alignment in space ([3], [4], [5]). However, this approach has the major drawback of not being able to accurately describe the facet surface (which is not planar). This is now possible with the presented novel approach by the use of subdivision surfaces. We do not present the detailed data set associated with the subdivision surface description of the facet joints here; instead we refer to the Visible Human Project [1], from which our model geometry is originated. The gap size was 0.4 mm for all motion segments.

The motion segment L4-L5, represented by subdivision surfaces, is shown in Figure 3(a). Here we used, in particular, the Catmull-Clark subdivision surface [2], which offers C2-continuity in the regular mesh domain and C1-continuity at irregular nodes. The contact stress distribution along the white dashed path starting from the inferior position `A' (see Fig. 3(a)) is plotted in Fig. 3(b). Therein, we compare the results for piecewise planar contact elements and for subdivision surfaces, both for different mesh densities.

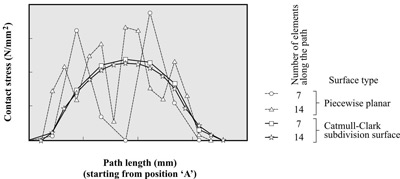Fig. 3: Contact stress distribution along a vertical path between the facet joints for different mesh densitites and contact surface continuities.